《数据结构与算法》第3章 栈(C语言)

3.1 栈的概述

同顺序表和链表一样，栈也是用来存储逻辑关系为 "一对一" 数据的线性存储结构。

栈存储结构与之前所学的线性存储结构有所差异，这缘于栈对数据 "存" 和 "取" 的过程有特殊的要求：

1.栈只能从表的一端存取数据，另一端是封闭的；

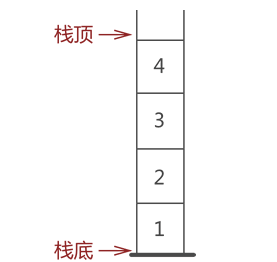
2.在栈中，无论是存数据还是取数据，都必须遵循"先进后出"的原则，即最先进栈的元素最后出栈。拿图 1 的栈来说，从图中数据的存储状态可判断出，元素 1 是最先进的栈。因此，当需要从栈中取出元素 1 时，根据"先进后出"的原则，需提前将元素 3 和元素 2 从栈中取出，然后才能成功取出元素 1。

因此，我们可以给栈下一个定义，即栈是一种只能从表的一端存取数据且遵循 "先进后出" 原则的线性存储结构。

通常，栈的开口端被称为栈顶；相应地，封口端被称为栈底。因此，栈顶元素指的就是距离栈顶最近的元素，拿下图 来说，栈顶元素为元素 4；同理，栈底元素指的是位于栈最底部的元素，下图中的栈底元素为元素 1。

基于栈结构的特点，在实际应用中，通常只会对栈执行以下两种操作：

• 向栈中添加元素，此过程被称为"进栈"（入栈或压栈）；
• 从栈中提取出指定元素，此过程被称为"出栈"（或弹栈）；

栈是一种 "特殊" 的线性存储结构，因此栈的具体实现有以下两种方式：

1.顺序栈：采用顺序存储结构可以模拟栈存储数据的特点，从而实现栈存储结构；

2.链栈：采用链式存储结构实现栈结构；

两种实现方式的区别，仅限于数据元素在实际物理空间上存放的相对位置，顺序栈底层采用的是数组，链栈底层采用的是链表。有关顺序栈和链栈的具体实现会在后续章节中作详细讲解。

栈的应用

基于栈结构对数据存取采用 "先进后出" 原则的特点，它可以用于实现很多功能。

例如，我们经常使用浏览器在各种网站上查找信息。假设先浏览的页面 A，然后关闭了页面 A 跳转到页面 B，随后又关闭页面 B 跳转到了页面 C。而此时，我们如果想重新回到页面 A，有两个选择：

• 重新搜索找到页面 A；
• 使用浏览器的"回退"功能。浏览器会先回退到页面 B，而后再回退到页面 A。

浏览器 "回退" 功能的实现，底层使用的就是栈存储结构。当你关闭页面 A 时，浏览器会将页面 A 入栈；同样，当你关闭页面 B 时，浏览器也会将 B入栈。因此，当你执行回退操作时，才会首先看到的是页面 B，然后是页面 A，这是栈中数据依次出栈的效果。

不仅如此，栈存储结构还可以帮我们检测代码中的括号匹配问题。多数编程语言都会用到括号（小括号、中括号和大括号），括号的错误使用（通常是丢右括号）会导致程序编译错误，而很多开发工具中都有检测代码是否有编辑错误的功能，其中就包含检测代码中的括号匹配问题，此功能的底层实现使用的就是栈结构。

同时，栈结构还可以实现数值的进制转换功能。例如，编写程序实现从十进制数自动转换成二进制数，就可以使用栈存储结构来实现。

3.2 顺序栈

3.2.1顺序栈概述

顺序栈，即用顺序表实现栈存储结构。通过前面的学习我们知道，使用栈存储结构操作数据元素必须遵守 "先进后出" 的原则，本节就给大家做详细介绍。

如果你仔细观察顺序表（底层实现是数组）和栈结构就会发现，它们存储数据的方式高度相似，只不过栈对数据的存取过程有特殊的限制，而顺序表没有。

例如，我们先使用顺序表存储 {1,2,3,4}，存储状态如图所示：

同样，使用栈存储结构存储 {1,2,3,4}，其存储状态如下图所示：

通过前面两图的对比不难看出，使用顺序表模拟栈结构很简单，只需要将数据从 a 数组下标为 0 的位置依次存储即可。

从数组下标为 0 的模拟栈存储数据是常用的方法，从其他数组下标处存储数据也完全可以，这里只是为了方便初学者理解。

了解了顺序表模拟栈存储数据后，接下来看如何模拟栈中元素出栈的操作。由于栈对存储元素出栈的次序有"先进后出"的要求，如果想将图中存储的元素 1 从栈中取出，需先将元素 4、元素 3 和元素 2 依次从栈中取出。

3.2.2顺序栈实现

顺序栈存储结构实现

栈是顺序表的一种，具有顺序表同样的存储结构，由数组定义，配合用数组下表表示的栈顶指针top(相对指针)完成各种操作。

#define MAX 100
typedef int data_t;  //定义栈中数据元素的数据类型
typedef struct
{
    data_t data[MAX];
    int top;  //指向栈顶位置（数组下标）的变量
}seqstack_t;  //顺序栈类型定义

【注】顺序栈也可以通过指针实现。

顺序栈的基本操作

(1) 顺序栈的初始化

顺序栈初始化很简单，只需要将栈顶设置为-1即可。

seqstack_t *CreateEmptyStack()
{
    seqstack_t *stack;
    stack = (seqstack_t *)malloc(sizeof(seqstack_t));
    stack->top = -1;

    return stack;
}

(2) 清空顺序栈

清空顺序栈是将栈顶设置-1。

void ClearStack(seqstack_t *stack)
{
    if(stack != NULL)
        stack->top = -1;
}

(3) 判断顺序栈是否为空

判断顺序栈是否为空是看栈顶是否为-1。

int EmptyStack(seqstack_t *stack)
{
    if(stack == NULL)
        return -1;
    return(stack->top == -1 ? 1 : 0);
}

(4) 判断顺序栈是否为满

判断顺序栈是否为满是看栈顶是否为MAX-1。

int FullStack(seqstack_t *stack)
{
    if(stack == NULL)
        return -1;
    return(stack->top == MAX-1 ? 1 : 0);
}

(5) 顺序栈入栈

对于顺序栈的进栈操作，首先判断栈为满，将新的数据元素存入栈内，然后将记录栈内元素个数的top+1即可。同时要保证底层数组的长度可以容纳新的数据元素。

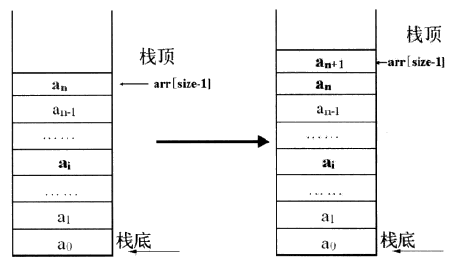
代码如下所示：

int PushStack(seqstack_t *stack ,data_t x)
{
    if(FullStack(stack))
        return -1;
    else
    {
        stack->top++;
        stack->data[stack->top] = x;
    }
    return 0;
}

(6) 顺序栈出栈

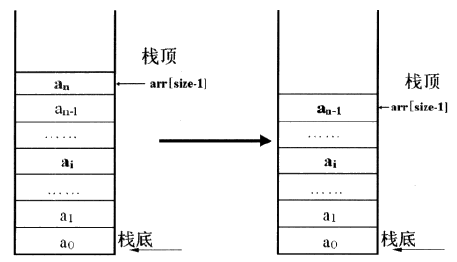
对于顺序栈的进栈操作，首先判断是否栈为空，让记录栈内元素个数的top-1。

int PopStack(seqstack_t *stack,data_t *x)
{
    if(EmptyStack(stack))
        return -1;
    else
    {
        *x = stack->data[stack->top];
        stack->top--;
    }

    return 0;
}

(7) 获取顺序栈栈顶元素

int GetTop(seqstack_t *stack,data_t *x)
{
    if(EmptyStack(stack))
        return -1;
    else
        *x = stack->data[stack->top];

    return 0;
}

(8) 释放顺序栈

void DestroyStack(seqstack_t *stack)
{
    if(stack != NULL)
    {
        free(stack);
    }
}

【完整代码参考3.1 seqstack】

3.3 链栈

3.3.1链栈概述

链栈，即用链表实现栈存储结构。

链栈的实现思路同顺序栈类似，顺序栈是将数顺序表（数组）的一端作为栈底，另一端为栈顶；链栈也如此，通常我们将链表的头部作为栈顶，尾部作为栈底，如图所示：

将链表头部作为栈顶的一端，可以避免在实现数据 "入栈" 和 "出栈" 操作时做大量遍历链表的耗时操作。

链表的头部作为栈顶，意味着：

• 在实现数据"入栈"操作时，需要将数据从链表的头部插入；
• 在实现数据"出栈"操作时，需要删除链表头部的首元节点；

因此，链栈实际上就是一个只能采用头插法插入或删除数据的链表。

3.3.2链栈实现

链栈存储结构实现

链栈和单链表的存储结构是相同的，只是链栈和单链表的实现不同罢了。

typedef int datatype;

typedef struct _node_
{
    datatype data;
    struct _node_ *next;
} linkstack;

链栈的基本操作

(1) 链栈的初始化

linkstack *CreateEmptyLinkstack()
{
    linkstack *s;

    s = (linkstack *)malloc(sizeof(linkstack));
    if(s == NULL)
    {
        return NULL;
    }
    s->next = NULL;

    return s;
}

(2) 判断链栈是否为空

判断链栈是否为空很简单，只需要判断stack->next是否为NULL即可。

int EmptyLinkstack(linkstack *s)
{
    if(s == NULL)
    {
        return -1;
    }
    return (NULL == s->next);
}

(3) 链栈入栈

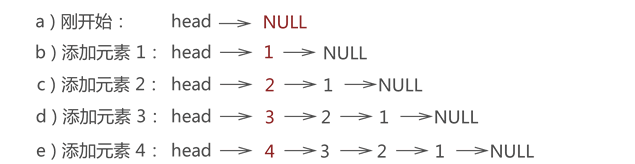
链栈入栈将各元素采用头插法依次添加到链表中，例如，将元素 1、2、3、4 依次入栈，每个数据元素的添加过程如图所示：

int PushLinkstack(linkstack *s, datatype x)
{
    if(s == NULL)
    {
        return -1;
    }
    linkstack *p;

    p = (linkstack *)malloc(sizeof(linkstack));
    if(p == NULL)
    {
        return -1;
    }
    else
    {
        p->data = x;
        p->next = s->next;
        s->next = p;
    }
    return 0;
}

(4) 链栈出栈

根据"先进后出"的原则，假设将元素 1、2、3、4 依次已经入栈，要先将元素 4 出栈，也就是从链表中摘除，然后元素 3 才能出栈，整个操作过程如图所示：

datatype PopLinkstack(linkstack *s)
{
    if(s == NULL)
    {
        return -1;
    }
    linkstack *p;
    datatype x;

    p = s->next;
    x = p->data;
    //方法一
    //s->next = p->next;
    //方法二
    s->next = s->next->next;
    free(p);

    return x;
}

(5) 清除链栈

void ClearLinkstack(linkstack *s)
{
    if(s == NULL)
    {
        return ;
    }
    linkstack *p;
    linkstack *temp = s->next;

#if 0
    while(temp != NULL)
    {
        p = temp->next;
        free(temp);
        temp = p;
    }

#else
    while (s->next != NULL)
    {
        p = s->next;
        //方法一
        //s->next = p->next;
        //方法二
        s->next = s->next->next;
        free(p);
    }
#endif

    s->next = NULL;

    return;
}

(6) 获取链栈栈顶元素

datatype GetTopLinkstack(linkstack *s)
{
    if(s == NULL)
    {
        return -1;
    }
    return (s->next->data);
}

(7) 释放链栈

void Destroylinkstack(linkstack *s)
{
    if(s != NULL)
    {
        if(EmptyLinkstack(s) != 1)
        {
            ClearLinkstack(s);
        }
        if(s->next != NULL)
            free(s->next);
        free(s);
    }
}

【完整代码参考3.2 linkstack】

代码获取方法

1.关注公众号[嵌入式实验楼]
2.在公众号回复关键词[Data Structures and Algorithms]获取资料